[UE4] 베지에 곡선(Bezier Curves), 에르밋/허밋 곡선(Hermite Curve), 캣멀롬 스플라인(Catmull-Rom Spline)

🎢 베지에 곡선(Bezier Curves)

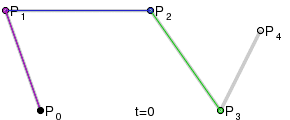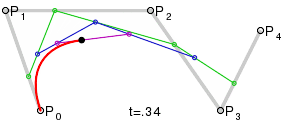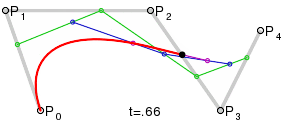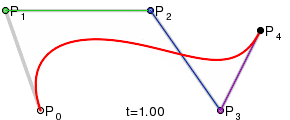1차 베지에 곡선	2차 베지에 곡선	3차 베지에 곡선	4차 베지에 곡선

 

 

3차 베지에 곡선

베지에 곡선이란 선분 위를 일정 속도로 움직이는 점과 그러한 점과 점을 잇는 또 다른 선분, 그리고 그 위를 일정 속도로 이동하는 또 다른 점 등을 조합해 최종적으로 특징 점이 그리는 궤적을 이용해 곡선을 그려내는 방법을 뜻한다.

🎢 에르밋/허밋 곡선(Hermite Curve)

3차 에르밋 곡선은 3차 베지에 곡선에서 변환 가능한 곡선으로, 4개의 점을 사용하는 대신 두 개의 벡터 U, V를 사용한다.

베지에 곡선의 또 다른 표현 방법으로봐도 무방하다.

🎢 캣멀롬 스플라인(Catmull-Rom Spline)

캣멀롬 스플라인은 포인트와 포인트 사이의 통과하는 포인트를 의미하는 특성을 갖는다.

캣멀롬 스플라인은 에르밋 곡선(Hermite Curve)를 활용하여 더 쉽게 곡선을 그리기 위해 착안된 방안이다.

에르밋 곡선에서 사용했던 U, V 벡터를 어떤 규칙으로 정하여 스플라인을 더 편하게 만들 수 있다.

 

즉, 시작(U)과 끝(V) 지점의 속도 벡터를 결정하기 위한 특정한 값을 가진 스플라인으로 새로운 스플라인이라기 보다는 3차 에르밋 스플라인을 구현하기 위한 기술이라고 보면 된다.

어떠한 각 지점들을 통과하는 곡선을 구현하려면 캣멀-롬 스플라인이 좋은 방법으로 사용될 수 있다.

 

캣멀롬 스플라인을 만드는 원리는 다음과 같다.

위 그림처럼 순서대로 연결될 A, B, C, D 정점을 U, V 벡터로 각각 이어 3차 캣멀롬 방식 스플라인이 만들어진다.

---

참조

https://blog.coderifleman.com/2016/12/30/bezier-curves/

중학생도 알 수 있는 베지에 곡선(Bezier Curves)

https://blog.naver.com/PostView.naver?blogId=kyuniitale&logNo=40022945907&redirect=Dlog&widgetTypeCall=true&directAccess=false 

베지어 곡선 (Bezier Curve)

https://tsyang.tistory.com/57

곡선(Curve) & 스플라인(Spline)

https://lee-seokhyun.gitbook.io/game-programming/client/easy-mathematics/gdc2012/catmull-rom-splines

캣멀-롬 스플라인(Catmull-Rom Splines) - Game Programming