[선형대수학] 벡터의 덧셈/뺄셈, 벡터와 스칼라의 곱셈

벡터의 덧셈: 벡터(x1, y1)와 (x2, y2)를 더하려면 각 벡터에 대응하는 성분 (x1+x2, y1+y2)를 더한다.

벡터 a가 (6,-2)이고, 벡터 b가 (-4, 4)라면 a+b 벡터는 (2,2)이다.

벡터 a의 머리에 벡터 b의 꼬리를 붙여 그래프에 나타내면 벡터 a의 꼬리와 벡터 b의 머리를 잇는 결과가 나온다.

반대로 더하는 순서를 바꿔 b+a 벡터를 구해도 결과는 같다.

벡터는 방향과 크기가 같다면 그래프 상 어디에 그려지든 같은 벡터이다.

 

벡터 a(2,1)과 스칼라 값(3)을 곱한다면 3a = 3 * (2,1)이 된다. 이후 각 벡터의 성분 2와 1에 3을 곱하면 3a = (6,3) 벡터가 된다.벡터와 스칼라의 곱셈 결과 바뀌지 않은 점은 "여전히 같은 방향을 가진다"는 점이다.
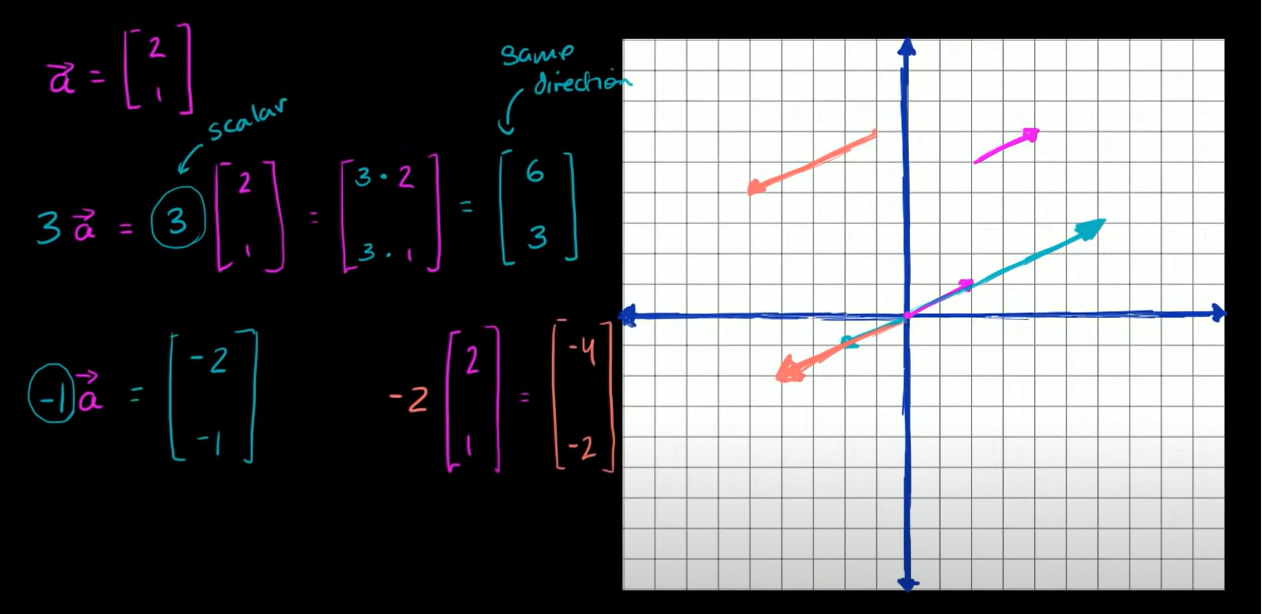
그러나 바뀐 점은 "크기가 3배로 늘어났다"는 점이다. 곱한 스칼라가 벡터의 크기를 확대했다고 생각하면 된다.

 

그렇다면 벡터 a(2,1)에 음수 -1를 곱한다면 -a = (-2, -1)가 될 것이다.이를 그래프 상에 표현했을 때 벡터의 방향을 완전히 뒤집었다.즉, 음수를 곱하면 벡터의 방향을 바꾼다.

 

벡터의 뺄셈은 간단하다. -1를 곱한 벡터를 더한다고 생각하면 쉽다.벡터 x(2,3)과 벡터 y(-4, -2)를 뺄셈하면 x(2,3) + -1y(-4,-2)와 같고, x(2,3) + y(4,2)와 같으므로 x-y는 (2+4, 3+2) = (6,5)가 된다. 이를 그래프상에서 그려보면 벡터 x,y의 각 머리를 이은 x-y 벡터가 그려진다.

---

(출처: 칸아카데미)