[프로그래머스/C++] 등굣길 (DP 문제 연습)

등굣길

문제 설명

계속되는 폭우로 일부 지역이 물에 잠겼습니다. 물에 잠기지 않은 지역을 통해 학교를 가려고 합니다. 집에서 학교까지 가는 길은 m x n 크기의 격자모양으로 나타낼 수 있습니다.

아래 그림은 m = 4, n = 3 인 경우입니다.

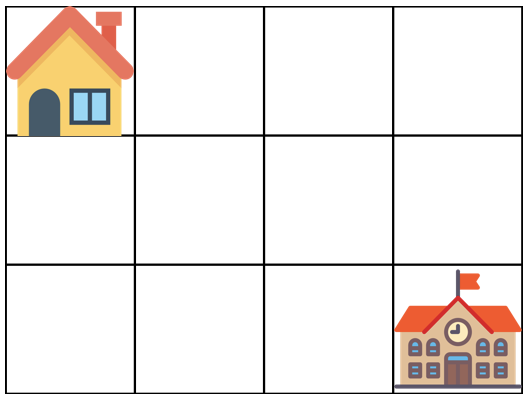
가장 왼쪽 위, 즉 집이 있는 곳의 좌표는 (1, 1)로 나타내고 가장 오른쪽 아래, 즉 학교가 있는 곳의 좌표는 (m, n)으로 나타냅니다.

격자의 크기 m, n과 물이 잠긴 지역의 좌표를 담은 2차원 배열 puddles이 매개변수로 주어집니다. 오른쪽과 아래쪽으로만 움직여 집에서 학교까지 갈 수 있는 최단경로의 개수를 1,000,000,007로 나눈 나머지를 return 하도록 solution 함수를 작성해주세요.

제한사항

• 격자의 크기 m, n은 1 이상 100 이하인 자연수입니다.
  • m과 n이 모두 1인 경우는 입력으로 주어지지 않습니다.
• 물에 잠긴 지역은 0개 이상 10개 이하입니다.
• 집과 학교가 물에 잠긴 경우는 입력으로 주어지지 않습니다.

입출력 예

m	n	puddles	return
4	3	[[2,2]]	4

 

입출력 예 설명

---

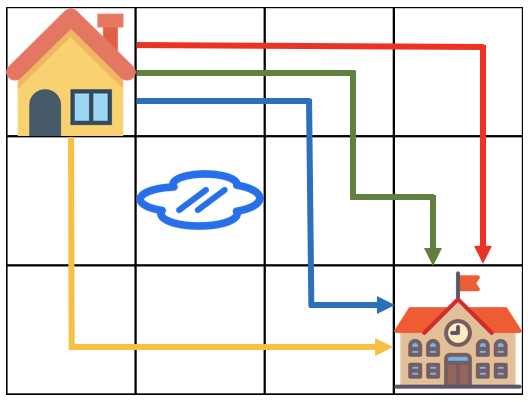
해당 문제는 동적계획법(DP)를 응용하여 시작점에서 끝지점으로 가는 최소 거리 경우의 수를 모두 구하는 문제이다.

 

 

시작점 (1,1)에 출발하는 집이 있고, (3, 4)에 도착하는 학교가 있을 때, 집에서 부터 for문을 돌려 검사를 수행하였다.

DP문제이기 때문에, 4x3 배열의 for문을 2중으로 전부 돌렸다.

 

먼저, 문제에 주어진 조건이 오른쪽 또는 아래로만 이동할 수 있기 때문에, 집에서 학교까지 가는 경로의 경우의 수를 구하기 위해선 왼쪽과 위를 향하는 경우의 수를 구하면 된다.

즉, (1,1) 인덱스부터 for문을 시작해서 왼쪽과 위로 가는 (x-1, y), (x, y-1) 인덱스의 경우의 수를 알면 된다.

 

1. 집에서 출발하는 시작은 1가지 경로로 시작하고, 물 웅덩이가 있는 경로의 개수는 미리 -1로 초기화한다.
1-2. 왼쪽과 위쪽 경로의 개수를 검사할 때, 경로가 -1개라면 물 웅덩이이므로 개수에 더하지 않는다.

2. 집에서 오른쪽 (1,2) 부터 검사를 수행한다. (1,2)에서 왼쪽과 위 경로의 개수는 1+0 이므로 결과는 1

3. (1,3)과 (1,4)의 경우도 전부 왼쪽의 1가지 경로만 검사되므로 경로의 총 개수는 1이다.

4. 학교 위쪽(2,4) 위치에서 보면 왼쪽 경로 1가지와 윗쪽 경로 1가지가 더해져 2가지 경로가 존재한다. 따라서 결과는 1+1 = 2

5. 학교의 왼쪽(3,3) 위치에서도 왼쪽 경로 1 + 윗쪽 경로 1 = 2가지 경로의 개수가 나온다.

6. 따라서, 학교 위치(3, 4)에는 왼쪽으로 들어오는 2가지 경로 + 윗쪽으로 들어오는 2가지 경로가 더해져 4가지 경로를 갖는다.

 

이러한 프로세스를 코드로 작성한 결과는 아래와 같다.

 

#include <algorithm>
#include <iostream>
#include <string>
#include <vector>

using namespace std;

int dp[101][101];

int solution(int m, int n, vector<vector<int>> puddles) {
    for (int i = 0; i < puddles.size(); i++)
		dp[puddles[i][1]][puddles[i][0]] = -1;

	dp[1][1] = 1;
	for(int i = 1; i <= n; i++)
	{
		for(int j = 1; j <= m; j++)
		{
			if (i == 1 && j == 1) continue;
			if (dp[i][j] == -1) continue;

			int a = 0, b = 0;
			if (dp[i][j - 1] != -1)
				a = dp[i][j - 1];
			if (dp[i - 1][j] != -1)
				b = dp[i - 1][j];

			dp[i][j] = (a + b) % 1000000007;
		}
	}
	return dp[n][m];
}

 

dp 배열을 최대 가로x세로 길이만큼 초기화하고, 물 웅덩이가 있는 곳은 미리 -1로 초기화하였다.

 

이후, 2중 for문을 수행하며 각 위치에서 왼쪽의 경로의 수(dp[i][j-1])와 윗쪽의 경로의 수(dp[i-1][j])가 물 웅덩이가 아니라면, 해당 경로의 수를 더하여 갱신해주었다.

 

이때, 문제에서 "집에서 학교까지 갈 수 있는 최단경로의 개수를 1,000,000,007로 나눈 나머지를 return" 하라고 되어있다는걸 생각하여, MOD 법칙에 의해 처음 값을 초기화할 때부터 나머지 연산을 수행해주었다.

 

 

만약, 나머지 연산을 dp 초기값 설정에서 미리 수행하지 않고, 최종 return되는 곳에서 수행한다면, 테스트케이스 정확성 검사는 만점이지만, 효율성 검사는 빵점이 나온다.

 

격자의 크기가 커서 경로의 수가 많이 나오는 경우 너무 큰 정수(10억, 1,000,000,007)의 나머지 연산의 중간 과정에 10억 7을 넘기기 때문이다.

 

⭐ M x N 크기의 격자에서 경로의 개수 구하기
M x N 크기의 격자에서 왼쪽 상단 시작점부터 오른쪽 하단 끝점까지 가는 경로의 수는 조합을 통해 계산할 수 있다.

(M+N) C (M) 이나, (M+N) C (N) 을 계산하면 경로의 수를 구할 수 있다.

예를들어, 20 x 15 크기의 격자에서 모든 경로의 수는 (20+15) C 20 혹은, (20+15) C 15 가 되는것이다.
이 값은 3247943160 로 매우 큰 경로의 수로 도출된다.

 

위와 같은 연산을 보면, 20x15 크기의 격자여도 30억이 넘는 경로의 개수가 나온다. 따라서 문제에 주어진 최대 크기 100x100의 경우엔 어마어마한 경로의 개수가 나올것이다.

 

이러한 경로의 개수를 나머지 연산으로 구할 수 없으므로, 해당 문제는 MOD 법칙(모듈러 법칙)을 모르고 있었다면 효율성 검사를 통과할 수 없는 나름 3단계의 문제였다.

---

📌 모듈러 법칙에 관한 설명은 이전 누적합 알고리즘 문제를 풀 때 정리한 적이 있다.

2023.08.17 - [💻코딩테스트/백준] - [백준/C++] 10986번 : 나머지 합 (누적 합)

[백준/C++] 10986번 : 나머지 합 (누적 합)

---

DP 문제는 언제나 정답 코드를 작성하기까지 너무 많은 시행착오를 겪게되는 것 같다. 점화식을 세우는 과정부터 헤매이다가 풀었는데 항상 결과는 간단하게 나와서 살짝 열받는 문제였다..ㅎㅎ

---

 

https://school.programmers.co.kr/learn/courses/30/lessons/42898

프로그래머스

https://ko.numberempire.com/combinatorialcalculator.php

조합 계산기