알고리즘 수업 - 피보나치 수 1
문제
오늘도 서준이는 동적 프로그래밍 수업 조교를 하고 있다. 아빠가 수업한 내용을 학생들이 잘 이해했는지 문제를 통해서 확인해보자.
오늘은 n의 피보나치 수를 재귀호출과 동적 프로그래밍으로 구하는 알고리즘을 배웠다. 재귀호출에 비해 동적 프로그래밍이 얼마나 빠른지 확인해 보자. 아래 의사 코드를 이용하여 n의 피보나치 수를 구할 경우 코드1 코드2 실행 횟수를 출력하자.
피보나치 수 재귀호출 의사 코드는 다음과 같다.
fib(n) {
if (n = 1 or n = 2)
then return 1; # 코드1
else return (fib(n - 1) + fib(n - 2));
}피보나치 수 동적 프로그래밍 의사 코드는 다음과 같다.
fibonacci(n) {
f[1] <- f[2] <- 1;
for i <- 3 to n
f[i] <- f[i - 1] + f[i - 2]; # 코드2
return f[n];
}입력
첫째 줄에 n(5 ≤ n ≤ 40)이 주어진다.
출력
코드1 코드2 실행 횟수를 한 줄에 출력한다.
예제 입력 1
5
예제 출력 1
5 3
예제 입력 2
30
예제 출력 2
832040 28해당 문제는 피보나치 수열을 풀이하면서 일반적인 재귀함수를 통한 함수 호출 횟수와, 동적 프로그래밍 방식을 이용한 함수 호출 횟수를 출력하는 문제였다.
우선 처음 풀이한 코드는 아래와 같다.
#include <algorithm>
#include <iostream>
#include <vector>
#include <string>
#include <cmath>
using namespace std;
int arr[41];
int FibCnt = 0;
int FibonacciCnt = 0;
int Fib(int n)
{
if (n == 1 || n == 2)
{
FibCnt++;
return 1;
}
else
return Fib(n - 1) + Fib(n - 2);
}
int Fibonacci(int n)
{
if (n == 1 || n == 2)
{
arr[n] = 1;
return arr[n];
}
if (arr[n] != 0)
return arr[n];
arr[n] = Fibonacci(n - 1) + Fibonacci(n - 2);
FibonacciCnt++;
return arr[n];
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
int n;
cin >> n;
Fib(n);
Fibonacci(n);
cout << FibCnt << " " << FibonacciCnt << "\n";
return 0;
}문제의 수도코드로 나와있는 내용을 구현하며 함수의 호출 Count를 직접 카운트하며 출력하였다.
시간초과나 다른 오류 없이 문제는 해결되었지만, 수도코드 내용을 구현하지 않고도 풀이할 수 있을 것 같아 다른 방법의 풀이도 고민해보았다.
첫번째 의사코드를 보면 결국 최종적으로 반환되는 1 값들의 합이 함수를 호출한 총 횟수가 된다. 또한 이는 피보나치 수를 계산해낸것과 같으므로 첫번째 의사코드는 N번째 피보나치 수와 같은 횟수만큼 실행된다고 볼 수 있다.
즉, 다섯번째 피보나치 수가 5라면, 코드 1의 실행 횟수도 5가 된다.
두번째 의사코드는 n이 1 또는 2라면 바로 1을 반환하기 때문에 함수 내용이 실행되지 않을 것이고, 3 이상의 수라면 반복문의 횟수만큼 함수가 실행 될 것이다.
즉, 3부터 N까지의 반복문이 실행되므로 총 N-2 회 실행된다.
문제의 조건에서 N 값은 5보다 크고 40보다 작기때문에 N-2를 출력해도 유효한 값만 출력된다.
#include <iostream>
#include <string>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n;
cin >> n;
int arr[41];
arr[1] = arr[2] = 1;
for(int i = 3; i <= n; i++)
arr[i] = arr[i - 1] + arr[i - 2];
cout << arr[n] << " " << n - 2;
return 0;
}
재귀함수를 사용하지 않고 두번째 수도코드의 내용만 반복문으로 구현한 후, 결과 값을 출력한 소스코드이다.
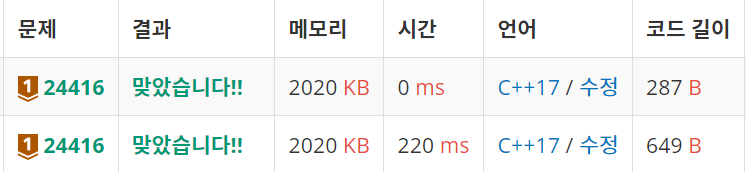
첫번째 코드에 비해 두번째 코드는 0ms 라는 시간이 출력되며 훨씬 빠르게 계산됨을 확인할 수 있었다.
'💻코딩테스트 > 백준' 카테고리의 다른 글
| [백준/C++] 2579번 : 계단 오르기 - DP/점화식 연습 (0) | 2023.06.12 |
|---|---|
| [백준/C++] 1003번 : 피보나치 함수 - 0과 1의 횟수 출력 (0) | 2023.06.11 |
| [백준/C++] 10757번 : 큰 수 A+B - unsigned long long을 넘는 자료형의 덧셈(string) (0) | 2023.05.30 |
| [백준/C++] 1193번 : 분수찾기 - 수학분류 (0) | 2023.05.30 |
| [백준/C++] 2566번 : 최댓값 - 2차원 배열에서 최댓값과 인덱스 찾기 (0) | 2023.05.22 |