트리의 지름
문제
트리의 지름이란, 트리에서 임의의 두 점 사이의 거리 중 가장 긴 것을 말한다. 트리의 지름을 구하는 프로그램을 작성하시오.
입력
트리가 입력으로 주어진다. 먼저 첫 번째 줄에서는 트리의 정점의 개수 V가 주어지고 (2 ≤ V ≤ 100,000)둘째 줄부터 V개의 줄에 걸쳐 간선의 정보가 다음과 같이 주어진다. 정점 번호는 1부터 V까지 매겨져 있다.
먼저 정점 번호가 주어지고, 이어서 연결된 간선의 정보를 의미하는 정수가 두 개씩 주어지는데, 하나는 정점번호, 다른 하나는 그 정점까지의 거리이다. 예를 들어 네 번째 줄의 경우 정점 3은 정점 1과 거리가 2인 간선으로 연결되어 있고, 정점 4와는 거리가 3인 간선으로 연결되어 있는 것을 보여준다. 각 줄의 마지막에는 -1이 입력으로 주어진다. 주어지는 거리는 모두 10,000 이하의 자연수이다.
출력
첫째 줄에 트리의 지름을 출력한다.
예제 입력 1
5
1 3 2 -1
2 4 4 -1
3 1 2 4 3 -1
4 2 4 3 3 5 6 -1
5 4 6 -1
예제 출력 1
11해당 문제는 트리의 지름을 구하는 문제이다. 트리의 지름은 트리에서 임의의 두 점 사이의 거리 중 가장 긴 것을 구하면 된다.
먼저, 입력으로 주어진 트리 그래프를 vector<pair<int, int>> graph[ ] 같은 배열에 vector 형태로 저장하였다. 이때 pair의 첫번째 값은 연결된 다음 노드이고, 두번째 값은 거리 값이다.
#include <iostream>
#include <string>
#include <vector>
using namespace std;
vector<pair<int, int>> graph[100001];
bool visit[100001];
int maxDist = 0;
int maxNode = 0;
void DFS(int node, int dist)
{
visit[node] = true;
if(maxDist < dist)
{
maxNode = node;
maxDist = dist;
}
for(int i = 0; i < graph[node].size(); i++)
{
int nextNode = graph[node][i].first;
int nextDist = graph[node][i].second;
if(!visit[nextNode])
DFS(nextNode, dist + nextDist);
}
}
int main()
{
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int V;
cin >> V;
for(int i = 0; i < V; i++)
{
int num, node, value;
cin >> num;
while(true)
{
cin >> node;
if (node == -1) break;
cin >> value;
graph[num].emplace_back(node, value);
}
}
DFS(1, 0);
fill(begin(visit), end(visit), false);
maxDist = 0;
DFS(maxNode, 0);
cout << maxDist;
return 0;
}
코드를 먼저 보자면, 문제에선 루트노드가 주어져있지 않지만 임의의 노드 1을 시작점으로 거리값이 가장 큰 노드를 찾아주었다. 이때, 최대 거리는 DFS 알고리즘을 사용하여 찾았다.
이후, 노드 1에서 가장 멀리 위치한 max Node로부터 다시한번 거리값을 계산하는 DFS연산을 한번 더 해주었다.
여기서 포인트는 임의의 노드에서 가장 멀리 위치한 노드를 찾고, 해당 노드에서 다시 최대 거리를 구하는 것이다.
이렇게 구한 최대 거리가 전체 트리의 지름이 될 수 있는 알고리즘 원리는 아래 블로그에 증명되어있어 참고하였다.
결과만 보자면, 트리의 지름을 구하고자 할 때 어떤 노드를 선택하든, 가장 멀리 위치한 노드를 찾고 그 노드의 최대거리를 구하면 된다.
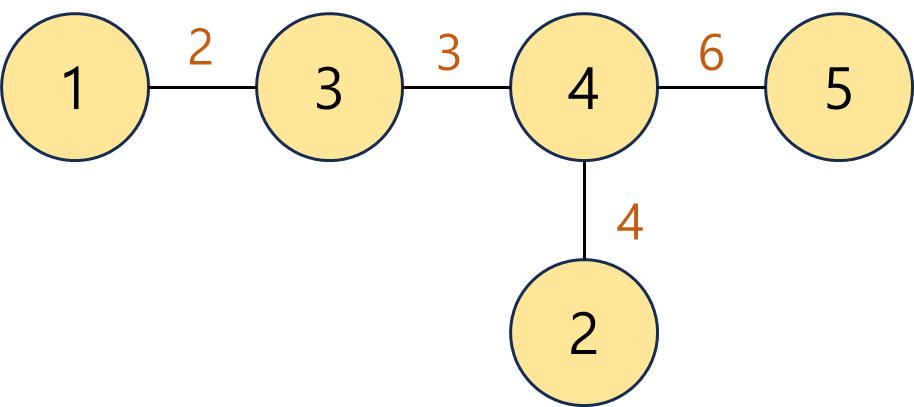
예제 입력 1의 경우를 그래프로 만들면 위와 같다. 트리이긴 하지만, 루트노드가 무엇인지 모르는 상황이기 때문에 내가 임의로 자리를 배치하여 그려주었다.
위에서 노드 1번에서 가장 거리가 긴 노드는 (1->3->4->5 = 2+3+6 = 11)인 5번 노드이다.
3번노드에서 가장 거리가 긴 노드도 (3->4->5 = 3+6 = 9)인 5번 노드이다.
4번노드에서 가장 거리가 긴 노드도 마찬가지로 5번이고, 나머지 2번 노드도 마찬가지이다.
반대로 5번노드에서 가장 거리가 긴 노드는 1번노드가 된다.
이렇게 1~4번 노드 어디에서든 가장 바깥쪽에 위치하여 거리가 긴 노드는 항상 5번 노드가 나오므로, 5번 노드에서 다시한번 거리가 긴 노드를 구하면 최종적인 트리의 지름이 구해지는 것이다.
나머지 과정은 단순한 DFS 구현이기 때문에 어렵지 않았다.
1167번: 트리의 지름
트리가 입력으로 주어진다. 먼저 첫 번째 줄에서는 트리의 정점의 개수 V가 주어지고 (2 ≤ V ≤ 100,000)둘째 줄부터 V개의 줄에 걸쳐 간선의 정보가 다음과 같이 주어진다. 정점 번호는 1부터 V까지
www.acmicpc.net
트리의 지름 구하기
트리에서 지름이란, 가장 먼 두 정점 사이의 거리 혹은 가장 먼 두 정점을 연결하는 경로를 의미한다. 선형 시간안에 트리에서 지름을 구하는 방법은 다음과 같다: 1. 트리에서 임의의 정점 $x$를
blog.myungwoo.kr
'💻코딩테스트 > 백준' 카테고리의 다른 글
| [백준/C++] 1504번 : 특정한 최단 경로 (다익스트라 연습) (0) | 2023.10.12 |
|---|---|
| [백준/C++] 1753번 : 최단경로 (다익스트라 연습) (0) | 2023.10.12 |
| [백준/C++] 11725번 : 트리의 부모 찾기 (DFS/BFS 연습) (0) | 2023.10.11 |
| [백준/C++] 14889번 : 스타트와 링크 (브루트포스 + 백트래킹 연습) (0) | 2023.08.24 |
| [백준/C++] 2206번 : 벽 부수고 이동하기 (BFS 심화 연습) (0) | 2023.08.19 |