🚩 회전변환

반지름의 길이가 1이고, 중심이 원점인 단위원을 좌표평면에 나타내고, θ를 나타내는 각도(동경)와 원 사이의 교점을 P(x, y)라고 하자.
점 P에서 x축에 수선을 그으면 직각삼각형이 만들어지며, 점 P의 좌표는 (cosθ, sinθ)가 된다.
단위원이 아니라 반지름이 a인 경우에는 점 P의 좌표가 (a*cosθ, a*sinθ)가 될 것이다.
회전변환은 어떤 한 점을 중심으로 잡고, 이동시키고자 하는 점을 회전시키는 변환을 의미한다. 즉, 원점을 중심으로 회전시킨다면 "원점을 중심으로 θ만큼 회전시키는 변환"으로 칭할 수 있다.
어떤 점에서 θ만큼 이동시키는 회전변환을 나타내는 행렬은 아래와 같다.
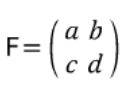
즉, 점 P를 (x, y)라고 하고, 회전이동된 점을 (x', y') 라고한다면 아래와 같이 표현이 가능하다.

실제로 점 P(1, 0)과 점 Q(0, 1)을 θ만큼 회전하여 회전변환된 점 P' 와 점 Q'를 나타낸 그림은 아래와 같다.

앞서 설명한 원리에 의해 점 P' 는 (cosθ, sinθ) 이고, Q' 는 (cos(90°+θ), sin(90°+θ)) 임을 알 수 있다.
이때 점 cos(90°+θ) = sin(-θ) = -sin(θ) 이고, sin(90°+θ) = cos(-θ) = cosθ 이므로,
점 Q' 는 (-sinθ, cosθ)로 표현할 수 있다.
즉, 점 P' 는 (cosθ, sinθ)이며, 점 Q' 는 (-sinθ, cosθ) 이다.
이것을 수식으로 나타낸 삼각함수의 항등식은 아래와 같다.


즉, 이렇게 구해진 a, b, c, d를 회전행렬로 변환식으로 합친다면

이와 같은 수식이 도출된다.

행렬을 각 요소에 대해 정리하면 위와 같은 x, y 좌표값이 나오며 이는 곧 점 P(x, y)를 각도 θ 만큼 회전시켜 P' (x', y')로 옮기는 회전변환을 나타낸다.
🚩 역변환
이때 회전변환의 역변환은 반대로 -θ 만큼 회전시키는 것이므로, 행렬에 θ 대신 -θ 를 대입하면 쉽게 역변환을 구할 수 있다.

참조
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=junhyuk7272&logNo=220140840595
7강 여러가지 변환(3) - 회전변환
4. 회전변환 어떤 한 점을 중심으로 잡고 이동시키고자 하는 점을 회전시키는 변환을 의미한다. &nbs...
blog.naver.com
https://color-change.tistory.com/54
(기하와 벡터) 회전변환 식 유도
::(기하와 벡터) 회전변환 식 유도:: - 개념, 공식, 증명, 유도 이 포스팅은 기하와 벡터의 회전변환 공식을 유도하는 글 입니다. 회전변환은 고교 수학(자연계) 기하와 벡터 과목의 전반부에서 처
color-change.tistory.com
'📚수학공부' 카테고리의 다른 글
| [수학] 삼각함수 항등식 (정의, 주기성, 대칭성, 이동, 덧셈정리) (0) | 2023.03.13 |
|---|---|
| [선형대수학] 외적(Cross Product) (0) | 2023.01.24 |
| [선형대수학] 벡터의 내적, 벡터의 길이 (0) | 2023.01.23 |
| [선형대수학] 선형결합, 선형생성, 선형독립, 선형종속 (0) | 2023.01.19 |
| [선형대수학] 단위벡터 (0) | 2023.01.17 |